パ:問題:2分割して円にする。の答えです。
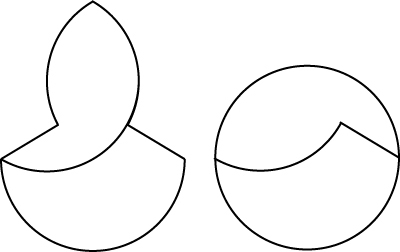
見てみるとそりゃそうだろうという感じだと思います。切り取った部分を120度回転することになります。
無理矢理でも論理的に考えてみると・・・。
左の図において中心の違う円弧が、ラクビーボール型の左、ラクビーボール型の右、下と3つある。
どんな分割をしても、円弧が2個乗るパーツができる。
そのパーツに乗った2つの円弧のうち最終の円周に使えるのは片方だけ。もう片方は、円の内部に収納されることになる。
とまぁ、ここまではどうにか。
追加:2007-07-13 19:30
答えまでたどりつける論理を発見。
1パーツに乗る2つの円弧、片方が円周、 片方が中に収納されるとすると組み合わせはラクビー右とラクビー左になる。(2つの円弧に下の円弧が含まれると円の範囲を飛び出すので)
下の円弧は全部円周に使うとして、円周がまだ、足らない。その部分をラグビー右で補うとすると答えのカタチにしかなりえないと。
- コメント (0)
- トラックバック (0)
- トラックバックURL :
- https://www.iwai-masaka.jp/tb.cgi/667








