前々々回の記事が、
だった。
底角15度の二等辺三角形は高校や中学の入試に出題されているとのこと。
斜辺の長さを1として、底辺の長さを求めてみる。夏休みの自由研究的なことで。
底辺の長さ=cos15度×2 なのだ。
これで答えになっている。(そして、このまま情報を保持するのが一番間違いが少ないと思う)
google検索で「cos15度」と入れると 0.96592582628
「cos15度*2」と入れると 1.93185165258 と出てくる。
で、これが、小数での答え。
小数ではなく、cosを使わないとするとどうなるか。
googleで「cos15度」と検索した下の方に、求め方の説明が何件も出てくる。
が、いくらか自力で解いてみるw
正三角形の半分の直角三角形から、cos30度は√3/2 とわかる。
cos30度とcos15度に「倍角の公式」を使ってみればどうにかなりそう。
「半角の公式」というのもあったような。
倍角の公式、半角の公式をgoogleで検索。
半角の公式 - 金沢工業大学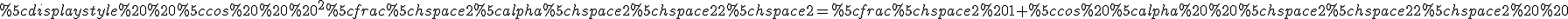
^{2}=\frac{1%2bcos30}{2})
^{2}=\frac{1%2b\frac{\sqrt{3}}{2}}{2})
^{2}=\frac{2%2b\sqrt{3}}{4})



より、半角の公式が
なので
で答えが出た。
googleに sqrt(2+sqrt(3)) と入れて検算すると1.93185165258であってる。
しかしだ、ルートの中にルートが入っているのは、はずせるものならはずすしておくしきたりだったような。
続く。
- コメント (0)
- トラックバック (0)
- トラックバックURL :
- https://www.iwai-masaka.jp/tb.cgi/56193









