■5次元以上
パズル懇話会メンバー白川さんに教わったこと、
多面体が4種類以上ある2次元、3次元、4次元が特別な場合。
多面体は、5次元以上は3種類しかない!!!!!
このことは、何回か読んだような気もするが、あらためて言われるとあらそうだったっけかといった感想。
■wikipedia
wikipedia先生に聞いてみよう。
http://ja.wikipedia.org/wiki/多胞体
http://ja.wikipedia.org/wiki/正多胞体
http://ja.wikipedia.org/wiki/ポリトープ
http://ja.wikipedia.org/wiki/4次元 アニメあり
「2次元以上のどの次元にも存在する3種類の正多胞体があり、標準正多胞体という。それぞれの標準正多胞体は、α体(正単体)、γ体(超立方体)、β体(正軸体)という」
http://ja.wikipedia.org/wiki/正単体
http://ja.wikipedia.org/wiki/超立方体
http://ja.wikipedia.org/wiki/正軸体
■納得する
■納得する
正単体は、線分-正三角形-正四面体-正五胞体 の系列
正単体を一次元分増やすには、どの頂点からも距離1の頂点を1個追加で納得していた。
超立方体は、線分-正方形-立方体-正八胞体 の系列
超立方体を一次元分増やすには、「増えた軸方向」に距離1の平行移動で納得していた。
正軸体については今まで、把握してなかった。
ちょっと考えた。
正軸体を一次元分増やすには、
中心から「増えた軸方向」に距離1と距離-1の点を2点とって、いままでの頂点と結べばよいのだ。
正方形-正八面体-正十六胞体の系列
次元が増えるにつれ頂点が2個づづ増えて行く。
■座標で把握
座標で表すとある意味、簡単で、
超立方体の頂点座標は
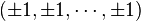
正軸体の頂点座標は

(正八面体の頂点の3D座標を手で入力しようしたとき「簡単じゃん」と思ったことと対応)
正単体は、1個次元をあげて、

なのだとほほう、なるほど。
■おまけ
立方体があったとき
頂点を一個決めるとその隣の頂点が3個あり、
それらを結ぶと正三角形ができる。
そうやってできる正三角形は8個ある。
なので・・・
n次元超立方体があったとき
頂点を1個決めるとその隣の頂点がn個あり、
それらを結ぶとn-1次元正単体ができる。
そうやってできるn-1次元正単体は(2^n)個ある。
うん、これはよさそう。
n次元超立方体の頂点を結んだときにできる
n-1次元正単体は全部で(2^n)個なのか。
つまり、違う結び方があるかないかだけど、それはなさそうなんだけど・・・。
- コメント (0)
- トラックバック (0)
- トラックバックURL :
- http://www.iwai-masaka.jp/tb.cgi/56071







