ミウラ折りは平行四辺形でできていることを知った。

なんか、もうちょっといじってみるよんということで。平行四辺形を直角二等辺三角形×２のものと正三角形×２のもので試してみた。平行四辺形の数としては５×５ということで。

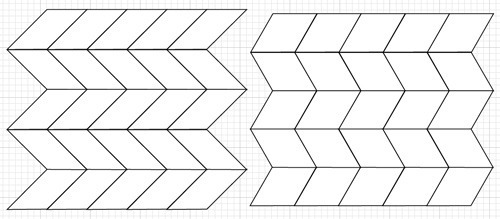
折りあげてみて。

たたんだものがこれ。

 

 たたんだときは、帯状に１直線に伸びる。これは、ミウラ折りのもともとの性質。平行四辺形のバリエーションを問わずこうなっている。このことには、普段のような、「平行四辺形がちょっとしか傾いてない場合」だと気づきにくい。

また、今回の二つは両方とも二等辺三角形×２の平行四辺形を使っているので、紙の重なりが、すっきりしている。
５×５のうちの上段の５×１のみで折った場合を考える。紙の重なりはどこもぴったり２枚となる。これは二等辺三角形×２であるため。