無四角タイルの非相似タイプのしきつめの図は

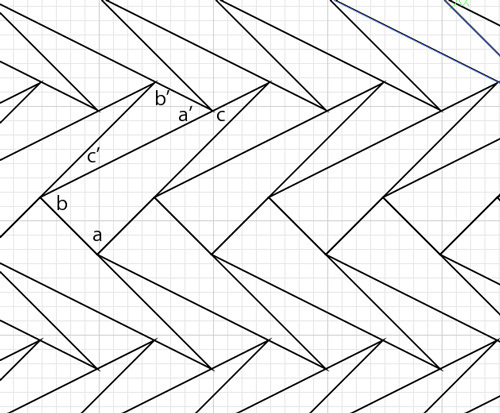
角度の関係を考えてみて、いっしょうけんめい計算すると全部b,cで表すことができて

１．
大きな方の三角形
(a,b,c)=(180-b-c,b,c)
小さな三角形
(a',b',c')=(b-c,180-b,c)

２．
二つの三角形が相似の場合は
b=b'のときで
b=180-b
b=90

大も小も(90-c,90,c)　となる。
つまり、直角三角形はすべてこのパタンにはまる。

３．
大三角形が二等辺三角形になるa=bのとき

b=180-b-c
c=180-2b

大は(b,b,180-2b)
小三角形は(3b-180,180-b,180-2b)

３－１．
ここで小三角形も二等辺三角形になるのは
3b-180=180-2b
5b=360
b=72

大(72,36,72)　小(36,108,36)

４．
大三角形が二等辺三角形になるa=cのとき
(c,180-2c,c)
小さい三角形は
(180-3c,2c,c)

４．１
ここで小さい三角形が二等辺三角形になるのは
180-3c=2c
5c=180
c=36
大(36,108,36) 小（72,72,36)
と
４．２
180-3c=c
4c=180
c=45
大(45,90,45) 小（45,90,45)

今回はこれまで。