無四角タイルの直角2等辺三角形の1:√2-1のときの並べ方の理解。
左側の3種類(緑、黄、赤)、回転、裏返しのバリーエーションで8種類の中から、はまるものを自由に並べていける。その際、四角は作らないように気をつける。
他の並べ方がないともいえない。
今、気づいたが、・・・。
8種類パーツを段々の向きで2種類に色わけすることもできる。
すると、上下方向に白黒白黒・・・とテンポよく並ぶ。
追加2011-05-21:
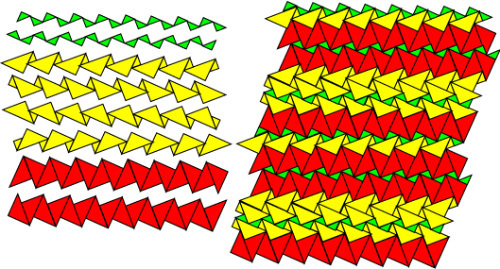
自分で「四角は作らないように気をつける」と書いといて、右の図は凹四角形が入っていた。(x_x;)
黄色のとなりに黄色がくることは×だった。
もう少し、考えてみると。
同じく緑のとなりの緑が×、赤のとなりの赤が×。
結局、同じ色を並べるなということに。
- コメント (4)
- トラックバック (0)
- トラックバックURL :
- https://www.iwai-masaka.jp/tb.cgi/55353
コメント
- Posted by かっちゃん
- at 2011/05/25 12:28:04
SSやMMやLLは不可。あとSLも凹四角形出現で不可でした。この他に直角二等辺三角形という意味では、新基本パタンの置き方があります。
- Posted by いわいまさか
- at 2011/05/25 13:11:45
訂正、ありがとうございます。②は失格パターンの方でした。また同じ間違いをしてしまいました。<(^^;)
(2)のルールは、正しくは、下図のように、
S,Lの隣はMかM*、M,M*の隣はSかL
ということですね。
S
/ \
M M*
\ /
L
---------------
最初のコメントに補足です。
S,Lは上下反転しても同じなので、(S+M-),(S+M*-)などが一致するのは、明らかでした。以上から、二列周期の場合は、等価でないのは、(SM)と(ML)の二種類となります。
---------------
ルール(1)があるので、周期的パターンは偶数周期に限られ、次に短いのは4列周期となります。SLの並びもないので、思ったより等価でないパターンは少なく、
(SMSM*),(SMLM),
の4種類で、(SMLM*)以外は、いわいさんご指摘のように、直角二等辺三角形の特殊性を使ったパターンになっています。
(SMLM*)は3角形が全てペアとなり、二種類の3角形に還元され、さらに一般の三角形でも可能なもう一つのパターンとなっています。このようなペアリングが可能な連結は、この(SMLM*)に限られそうなので、他の三角形にも適用できそうなパターンは、列の組み合わせを変えても、もう無いような気がします。
- Posted by かっちゃん
- at 2011/05/25 17:39:26
(SMLM*)は新基本パタン(非相似)の2倍体。
- Posted by いわいまさか
- at 2011/05/25 19:16:15









とても理解しやすい連結方法だと思います。,M*+,L+,L-
+-は必ず交互なので、+-を省略しても良いかな?
これを元に、さらにテキストベースでも理解を容易にするために、上から順に
S+,S-,M-,M+,M*-
と名前を付けてみました。SMLはサイズを、+-は左右反転の関係を、*は上下反転の関係を表したつもりです。
連結のルールは,上で言っていることと同じですが、以下の二つで表せます。
(1)+-交互に並ぶ
(2)同じ文字が隣接しない
連結パターンを考える場合、
X+Y-とX-Y+は左右反転で等価、X+Y-とY+X-は上下反転で等価となるので、二種交互に並べる方法は、下記の五種類に限られ、既出の3種のパターンに帰着します。
①大△1+小△3のパターン(基本パターンの拡張)
=(S+M-),(S+M*-)
②大△2+小△2のパターン(新パターン)
=(S+L-)
③大△3+小△1のパターン(基本パターンの拡張)
=(M+L-),(M*+L-)
#