前回の問題は
「三角形１種類（裏返しはあり）で平面を敷き詰めてください。
 その同じ平面を２枚もってきて重ね合わせます。
平行移動、回転移動は可能です。
 でも結局、線がピッタリ重なりあう場所が、平行移動も回転移動もまるっきりしてない、元の場所しかないようにしてください」

　答えはたくさんあるわけで、ここでは、いわいがみつけたパタンを紹介する。

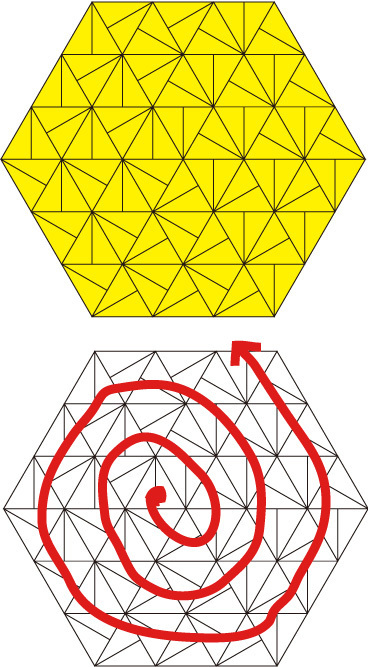
　正三角形を２分割した三角形１種類（裏表はあり）で敷き詰めてある。

　上の図を見ても分割の方向があっちこっちいっているようで何のこっちゃだが。

　下の図のように分割線の方向をつなげてある。
　らせん状にどんどん敷き詰めていける。
　が、いわゆる、単純なくりかえしと違って、平行移動や回転移動してももとの図と重なることはない。
　何しろ、赤線の出だしているヘソがあるわけで。

　この敷き詰めの特長のもうひとつは平面のどんなところにほうりだされても、分割線の方向にそって歩いていけばヘソに必ずたどりつくこと。

　逆問題としては、「この図が答えになるような問い方でなんかいいのはあるだろうか？」。