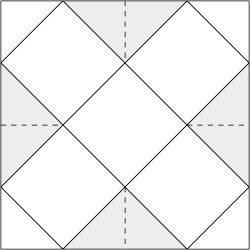
答えは次の図、実線が山線、点線が谷線。灰色の部分が中に折りこまれる余剰部分。Ototoさんがコメントで答えてくれたとおり、立方体の１辺の長さは√２／４＝0.353553391。



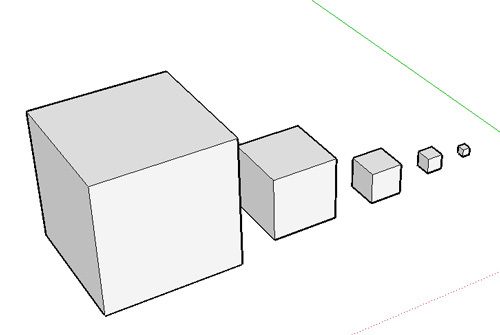
　実際、折り紙で作ってみた図。
オレンジ：立方体　　　いわい作
キミドリ： 正八面体　　ちゃーりー作
ミドリ：　 立方八面体へこみつき　ちゃーりー作

 

　１番上の展開図において灰色部分があまるのでそれを切り取ってはぎあせると面積１／４の正方形ができる。それを使って同様に立方体を作るとあまりが面積１／１６で・・・・という図。
 
　　
  この問題、すっきりした問題だったので既知なのでは？と思い、パズルのメーリングリストに、聞いてみた。情報がたくさん得られたので、掲載、ほぼ原文のまま。

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

正方形から展開図を切り出すというのを考えた事がある。
立方体の面がつなぎ合わさっていても良いという展開図。

小谷善行

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

私もこの問題は考えたことがあります。それに、長方形（もちろん正方形を含む）でいろいろな立体をラッピングする問題は、確か10年ほど前にパズ懇ニュースに取り上げられていた気がします（正方形の紙で立方体をラッピングする問題は、岩井さんの問題と等価です）。まあ私のその記憶の定かはともかく、少なくともセルヒー・グラバルチュクは、この問題を含めたかなりさまざまな問題を出題し、いちおうの答えも出しています。私の知る限り、彼が扱っているのは以下の6×4＝24通りの問題です。
ラッピングされるもの…正三角形板、正方形板、正六角形板、
　　　　　　　　　　円板、正四面体、立方体
ラッピングする紙の形…正三角形、正方形、正六角形、円
彼のAge of Puzzles: Paperfoldings, 2005参照。

岩沢宏和

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

昨年12月20日(厳密には21日)放送の「たけしのコマネチ大学数学科」
テーマ：ラッピング　の問題が同じかな？
以下、その問題
――――――――――――――――――――――――――――――
１辺が10cmの立方体の箱を１枚の長方形の包装紙で包む時、その最小面積を求めなさい。ただし立方体の表面がどの部分も覆われていてかつ包装紙の裏面が表側に現れてはいけません。また長方形の紙にハサミで切り込みを入れてもいけないものとします。
――――――――――――――――――――――――――――――
小田原充宏

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

岩井さんの問題に限定して、セルヒーの情報の受け売りでもう少し述べると、少なくとも以下では扱われています。
・マーチン・ガードナーのMathematical Magic Show, 1977
・http://www.mathpuzzle.com/wrap.htm
・http://www.mathematische-basteleien.de/oricube.htm
・http://erikdemaine.org/wrapping/

岩沢宏和

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

この問題は、平面を折って立体を作る（包む）とか、立体の表面を開いて平面を作るなど、広くみると平面と立体（の表面）との関係に関わる問題ですね。おりがみやペーパークラフトもその一環。以前NOBOXで話題になった、「三角形を折って四面体を作る」問題などもその一つ。
Cube wrapping, Polyhedron wrapping, cube folding, polyhedron folding, cube unfolding,ｐolyhedron unfolding などのキーワードで検索するといろいろ出てきます。

MITのErik Demaine（先週アメリカで会いました）の多面体（円盤を含む：これ２面体？）を平面で包む問題についてのWrapping Polyhedraという一般的な概観のメモもwebで読めます。
http://erikdemaine.org/wrapping/
ここには、色々なリンクが張られていて、その世界の概観がある程度理解できそうですので、是非見て下さい。なお、
http://courses.csail.mit.edu/6.885/fall04/erik_notes/100dpi/L8-3.html
http://courses.csail.mit.edu/6.885/fall07/lectures/L12.pdf
などにも、彼の立方体の正方形によるラッピングの手書きの講義ノートが示されています。

高島直昭

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃
以上