前回はプ:フラクタルで3D。
■3Dでドット打ちはきつい
1辺1000の正方形を1辺1の正方形で埋めるためには1メガ個要る。
1辺1000の立方体を1辺1の立方体で埋めるためには1ギガ個要る。
2Dだとドット打っていくと絵になるけど、3Dだと埋め尽くせないぐらいの空間がある。しかもカメラ・視点の移動も入ってくるし。ドットで打っていくような方法は止めた。
■全体を部分にコピーする方法
代わりに全体を複数個「縮小コピー移動回転」して、次の世代の全体を作ることにした。
複数個のところを2個とすると
自分=自分の1/a縮小コピー回転移動+自分の1/b縮小コピー回転移動 (※)
となる。
自分に対しての方程式だと思って解くと答えになるがその答えはどんなに顕微鏡で大きくしてもいつまでも複雑な3Dフラクタルそのものになるわけで。
■話は少しそれてルート5を求める話
こんな式がありました。
x = (5/x +x)/2
xを計算して求めると
2x=5/x +x
x = 5/x
x^2=5
x=±√5
それとは別に右辺のxに適当な数字を入れて計算した値を新しいxとし、それを繰り返していくと
((5 / 1) + 1) / 2 = 3
((5 / 3) + 3) / 2 = 2.33333333
((5 / 2.33333333) + 2.33333333) / 2 = 2.23809524
((5 / 2.23809524) + 2.23809524) / 2 = 2.2360689
((5 / 2.2360689) + 2.2360689) / 2 = 2.23606798
・・・・・
「富士山麓オオム鳴く」と見事に√5の数値が求まって来ている。
■そんな感じで
上記式(※)を√5の数値を求めたような感じでアプローチしていこうということ。
√5の場合は数値が段々正確になっていったけど、最初に適当なポリゴンを置いて、それが段々、詳細になっていく路線で。自分を元に計算すると新しい自分ができて、さらにその自分を元に計算するとまた新しい自分が・・・。
実は、前回のIFSの方法と今回の方法とは第0世代がドットかポリゴンかが違うだけというとらえ方もできる。
■C++⇒MELスクリプト
あと、C++で書いた実行ファイルでMELスクリプトを出力する方法を当面は取ろうと思う。MELスクリプトのみで手で書ききれるような気もするが、C++の方が何かと便利で「乱暴ができる」ので。とりあえず、「自分」の第0世代目を描いてみた。底がない三角形ポリゴン4枚によるピラミッド。
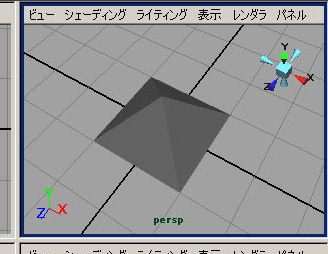
つづく
20080208 パズルっぽいけど投稿ジャンルはプログラミングに変更。
- コメント (0)
- トラックバック (0)
- トラックバックURL :
- http://www.iwai-masaka.jp/tb.cgi/41869







