円を１０個の合同図形にわけて、1つずつのパーツを左右対称にしろと言われれば、まずはレモン型に切ることが考えられる。

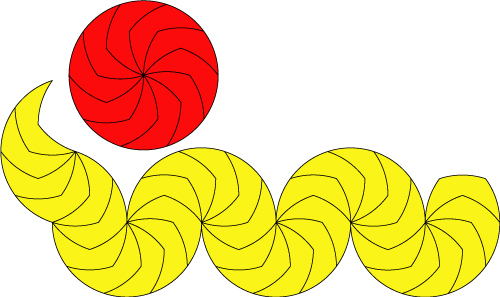
　他にはというと図の赤い円のようにできる。パ：正十角形分割答え２個の応用ということになる。先週までの流れがなくて、いきなり出されるとかなりの難問だ。

　黄色い蛇のような図はパーツを適当につなげてみたところ。

　下の赤い円を変形して、左右対称・２１個あるコーナーの点の位置は保ったままもっと面積を大きくすること（円ではなくなるが）ができる。その場合の最大はどうなるかという問題が考えられる。